Tome un galón de leche y agítelo hacia arriba y hacia abajo moviendo solo la muñeca.

Luego, extienda el antebrazo y agítelo moviendo solo el codo.

Luego, extienda todo el brazo y sacúdalo moviendo solo el hombro.

La masa no cambió, pero la fuerza que se necesitó para moverla aumenta (¡mucho!) porque está más lejos de ti. Este fenómeno, cuando se hace referencia a la rotación de una masa (como girar alrededor de la muñeca, el codo o el hombro) se denomina "momento de inercia" o, específicamente , el " momento de inercia de la masa ".

De manera similar, se vuelve "más difícil" aplicar la misma fuerza a cualquier cosa cuanto más lejos del origen de la fuerza se obtiene. En casos distintos de la masa específicamente, como en las vigas en I o en las vigas de madera, la propiedad de interés se denomina "momento de inercia del área" o, para aumentar la confusión, también " segundo momento del área ".

Esencialmente, cuanto más material (área de la sección transversal) pueda alejar de la fuerza, menor será el impacto que la fuerza tiene sobre el material. Es muy similar a cómo tu hombro tiene que trabajar tan duro para sacudir la leche.

También puedes considerar que, para un arco de movimiento dado, el material atravesado por ese arco aumenta linealmente con la distancia, y así También podría considerar que su fuerza se aplica a más material (aunque esto no es técnicamente correcto), y debido a que se aplica a más material, la fuerza efectiva disminuye.

:EDIT:

Hice una imagen (no animada, lo siento) que muestra un arco atravesado, y cómo permanece constante si el ángulo atravesado disminuye linealmente al aumentar la distancia .

El objetivo de este gráfico es demostrar tensión. Si su hombro hiciera el mismo trabajo que su muñeca, entonces el galón de leche subiría y bajaría la misma distancia lineal , pero no atravesaría el mismo ángulo .

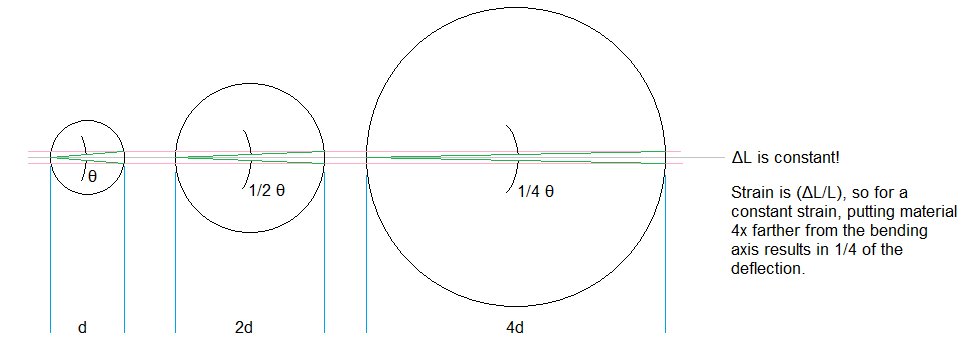
De manera similar, si intenta doblar algo, como en una viga de piso, el cambio de longitud (deformación) en el material puede ser el mismo, pero si puede colocar el material más lejos del eje de curvatura, esa deformación corresponde a una deflexión más pequeña.

Probemos con un ejemplo numérico. Considere una viga rectangular muy corta y muy ancha cuyo ancho de sección transversal es de 10 my altura de sección transversal es de 0,1 m. Esta viga es representativa de un corte, pero la estoy usando para este ejemplo para, con suerte, conducir el punto.

El momento de inercia del área de la viga alrededor de su eje x ($ I_x $) está dado por:

$$ I_x = \ frac {bh ^ 3} {12} \\ I_x = \ frac {(10) (0.1 ^ 3)} {12} \\ I_x = 0.000833 \\ $$

El El momento de inercia del área de la viga es muy pequeño alrededor del eje x; es muy fácil "girar" alrededor del eje x.

Ahora, usando el teorema del eje paralelo, configurémoslo a una distancia de 1 m del eje de flexión. Esto significa que el momento de inercia del área alrededor del eje de flexión es:

$$ I_x = I_ {x '} + Ad_y ^ 2 \\ I_x = 0.000833 + (1) (1 ^ 2) \\ I_x = 1.000833 \\ $$

Entonces, puede ver, el momento de inercia del área para flexión es aproximadamente 1 para este ejemplo, donde la distancia de la viga al eje de flexión es 1. Ahora, si la viga se mueve a una distancia de 2 m desde el eje de flexión, el teorema del eje paralelo da que el nuevo momento de inercia del área sea:

$$ I_x = I_ {x ' } + Ad_y ^ 2 \\ I_x = 0.000833 + (1) (2 ^ 2) \\ I_x = 4.000833 \\ $$

Entonces, cuando la distancia se duplica, el momento de inercia del área aproximadamente se cuadruplica. Ahora, considere la tensión de flexión:

$$ \ sigma = \ frac {My} {I} \\ $$

El momento de flexión, multiplicado por la distancia desde el eje de flexión, dividido por el momento de inercia del área. Ahora, para el primer ejemplo, la viga estaba a 1 m, y el momento de inercia del área era aproximadamente 1. Esto significa que la tensión es de aproximadamente $ \ sigma = \ frac {M (1)} {(1)} $, o $ M $.

Cuando la viga se mueve a 2 m, el momento de inercia se vuelve aproximadamente 4, pero ahora la distancia $ y $ para llegar a esa viga es de $ 2 $, por lo que la tensión de flexión se convierte en aproximadamente $ \ sigma = \ frac {M (2)} {4} $, o $ \ frac {1} {2} M $. Al colocar la viga al doble de la distancia, la tensión de flexión se redujo a la mitad. La deformación está relacionada linealmente con la tensión por el módulo de Young (asumiendo deformación elástica), por lo que esto significa que la deformación, o alargamiento, también se reduce a la mitad moviendo la viga el doble de lejos.

De nuevo, este fue un ejemplo ilustrativo en el que elegí el tamaño de la viga para llevar el momento de inercia del área de la viga a un valor insignificante, de modo que el teorema del eje paralelo fue el factor dominante. Esto se hizo para reforzar el concepto de que el material colocado más lejos del eje de flexión produce menos tensión (y por lo tanto, menos deformación / flexión) en el borde del material.

La web o parte ancha del 2x10 es la parte que resiste la flexión. ¿Un 2x más ancho? o la red resistirá doblarse bajo cargas más pesadas. La fuerza que se transfiere a través de la banda significa que es necesario estirar o comprimir más material para que falle.

Imagínese doblando un 2x10 en un plano con la parte de 10 pulgadas. La parte inferior se estirará a lo largo de la viga y la parte superior se comprimirá. Tener más material para resistir esas fuerzas hace que la viga (o viga en I) sea más fuerte. Usar un 2x10 con la banda hacia arriba tendría muy poco material que resista el estiramiento o la compresión, lo que conduciría a fallas mucho más fácilmente.

En el contexto de los cálculos de ingeniería, esto se debe a una propiedad llamada 'segundo momento del área', la forma en que se define es un poco obtusa pero describe algo que es razonablemente intuitivo.

Si considera una viga, sostenida en ambos extremos con un peso en un punto en el medio (obviamente) se doblará. Esta fuerza de flexión trata de estirar el borde inferior y comprimir el borde superior, por lo que, lógicamente, hay una línea a lo largo del medio donde no se dobla ni se comprime y, de manera similar, la mayor tensión está en el borde superior e inferior, disminuyendo hacia el medio.

Si hace el análisis completo, resulta que la rigidez de la viga es directamente proporcional a su ancho, pero también al cubo de su profundidad.

Entonces, en términos de flexión, la distancia entre la línea central y el borde de una viga (en la dirección de carga) es mucho más importante que solo su área de sección transversal.

Por extensión, el material cerca de la línea central contribuye mucho menos a la rigidez que el material cerca del borde y algo así como una viga en I es solo una forma de prescindir de gran parte de este material que está agregando masa pero no contribuyendo mucho a la rigidez.

Lo primero que hay que tener en cuenta es cómo se acumula el estrés en un material. Esto es bastante intuitivo y es algo que todos sabemos, pero requiere un poco de pensamiento para respaldarlo matemáticamente. Es bastante fácil dejarse atrapar por el mundo del 'Segundo momento del área', que es increíblemente importante para los cálculos, pero no es estrictamente necesario para comprender cómo funciona (escucho gritos de "herejía" ..).

Básicamente, cuando una viga se dobla, las fibras inferiores se estiran y separan ( tensión ), mientras que las fibras superiores se aplastan ( compresión ). La viga fallará (por ejemplo, se romperá) cuando las fibras superiores alcancen su resistencia máxima a la compresión o las fibras inferiores alcancen su resistencia máxima a la tracción . ¡Realmente simple! Vea mi boceto vquick a continuación:

Entonces, las implicaciones de esto es que en algún punto entre las fibras inferior y superior, hay una punto donde no hay tensión (donde pasa de tensión a compresión). El momento de flexión máximo (charla del ingeniero, ¡no es estrictamente importante para comprender!) Que puede soportar una viga está limitado por la resistencia a la compresión o tracción de una viga, por lo que trabajando hacia atrás podemos calcular la diferencia entre una viga que está de pie uno acostado.

Hice un cálculo manual rápido con algunas suposiciones (para simplificar, asumí que la viga fallará en compresión y tiene una resistencia a la compresión de 10N / mm ^ 2 y cambié la viga de 2 " x10 "a 20 mm x 100 mm). A partir de esto, puede calcular el "área" del triángulo de tensión. Luego, multiplique esto por el área de la viga sobre la que se encuentra este triángulo de tensión.

Como puede ver, la 'más alta' de las dos vigas tiene un triángulo de tensión más grande y, por lo tanto, puede resistir más flexiones. Esto se debe a que más de la viga se encuentra más lejos del eje neutral (el punto donde la viga no está ni en compresión ni en tensión). Básicamente, si aumentara lentamente la carga, la fibra superior de la viga más alta tardaría más en alcanzar el límite asesino de 10N / mm ^ 2 que le he dado.

Espero que esto sea claro y simple, es un poco irritante explicar lo que es un concepto relativamente simple porque hay mucho terreno por recorrer.

EDITAR: Planeo volver a hacer esos bocetos / cálculos pronto, con suerte con algo de color. Los dibujé rápidamente en el trabajo, ¡así que no les puse mucho esfuerzo!

Todos los materiales estructurales colapsan cuando sufren deformaciones y tensiones excesivas. Si estira demasiado un elástico, se romperá.

Las vigas se consideran elementos de viga. Esto significa que la fuerza interna primaria que necesitan soportar es el momento flector. Este momento de flexión es resistido por un par de fuerzas dentro de la viga. El momento provoca una rotación de la viga: la parte superior de la viga se comprimirá y la parte inferior se estirará. Esto significa que el par de fuerzas estará compuesto por la fuerza de compresión total en la mitad superior de la viga y la fuerza de tracción total en la mitad inferior (que debe ser igual en flexión simple).

Ahora, el El momento debido a un par de fuerzas es igual al producto de una de las fuerzas por la distancia entre ellas. Por lo tanto, para una vigueta colocada en la configuración fuerte ("alta") en oposición a la configuración débil ("ancha"), la distancia será mayor, lo que significa que se reducirán las fuerzas necesarias para soportar el momento de flexión. Dado que, al final del día, lo que hace que el elemento colapse son las tensiones excesivas, desea minimizar las fuerzas internas totales de compresión / tracción (y por lo tanto las tensiones) y, por lo tanto, siempre coloque los elementos en su configuración "fuerte". >

Una viga reacciona al momento de flexión doblando un poco en la dirección del momento. Esta flexión crea tensión en la sección transversal de la viga, tensión en la cara inferior y compresión en la cara superior. La deformación es directamente proporcional al estrés.

Por simplicidad, supongamos que hemos doblado una viga que tiene 1 cm ² de material en la parte superior e inferior y una red de 10 cm de ancho y la tensión máxima que este material es capaz de resistencia es de 1 kg / cm ² .

Entonces, el momento máximo que puede soportar esta viga es de 1 kg x 10/2 en la parte superior y 1 kg x 10/2 en la parte inferior, en conjunto, puede soportar 1 kg x 10 cm = 10 kgcm de impulso.

Si ensanchamos la viga para que la red tenga 20 cm de ancho pero la misma cantidad de material, la nueva viga nuevamente tiene 1 cm ² de material en la parte superior y 1 cm ² material en la parte inferior. Pero esta viga puede soportar 1 kg x 20 cm = 20 kgcm de impulso. ¡Darle la vuelta a la viga aumentará efectivamente el ancho de su banda!

¿Por qué orientamos las vigas del piso con el lado más largo verticalmente? como en la forma de la letra "I"?

Como se mencionó en otras publicaciones, el nombre de la teoría es "momento de inercia masivo" del cual hay libros de texto completos para explicar.

Sin embargo, simplemente, la fórmula para calcular este momento de inercia (para un rectángulo como una viga de 2x10) es (bh ^ 3) / 12 o en inglés "B" x "H Cubed" sobre 12.

cuando la viga está orientada de esta manera, su lado más largo (10 ") está orientado como la" H "(y la base es 2). Por lo tanto, cuando se orienta de esta manera, la madera resiste cargas mucho más pesadas que si fuera "acostado".

Intente doblar una regla de plástico de diferentes maneras. Hay una forma que será muy difícil. ¡Esto se explica por el momento de inercia!

La razón por la que Las vigas son tan delgadas en el medio que pueden retener su fuerza en esta orientación, pero para ahorrar peso, su diseño es mínimo (porque el peso de la viga también aumenta las fuerzas que deben calcularse). ¿Por qué harías la viga más pesada de lo que es? eds a ser si es tan fuerte sin el peso extra?